Gordon Ma, Dimitris G. Angelakis
Qubit-efficient optimization seeks to represent an 
-variable combinatorial problem within a Hilbert space smaller than 
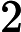
, using only as much quantum structure as the objective itself requires. Quadratic unconstrained binary optimization (QUBO) problems, for example, depend only on pairwise information — expectations and correlations between binary variables — yet standard quantum circuits explore exponentially large state spaces. We recast qubit-efficient optimization as a geometry problem: the minimal representation should match the 
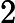
structure of quadratic objectives. The key insight is that the local-consistency problem — ensuring that pairwise marginals correspond to a realizable global distribution — coincides exactly with the Sherali-Adams level-2 polytope 
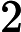
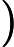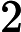
, the tightest convex relaxation expressible at the two-body level. Previous qubit-efficient approaches enforced this consistency only implicitly. Here we make it explicit: (a) anchoring learning to the 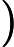geometry, (b) projecting via a differentiable iterative-proportional-fitting (IPF) step, and (c) decoding through a maximum-entropy Gibbs sampler. This yields a logarithmic-width pipeline (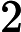
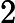
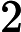qubits) that is classically simulable yet achieves strong empirical performance. On Gset Max-Cut instances (N=800–2000), depth-2–3 circuits reach near-optimal ratios (
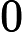
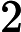
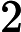
), surpassing direct baselines. The framework resolves the local-consistency gap by giving it a concrete convex geometry and a minimal differentiable projection, establishing a clean polyhedral baseline. Extending beyond naturally leads to spectrahedral geometries, where curvature encodes global coherence and genuine quantum structure becomes necessary.
Cite as BiBTex
@misc{ma2025informationminimalgeometryqubitefficientoptimization,
title={An Information-Minimal Geometry for Qubit-Efficient Optimization},
author={Gordon Ma and Dimitris G. Angelakis},
year={2025},
eprint={2511.08362},
archivePrefix={arXiv},
primaryClass={quant-ph},
url={https://arxiv.org/abs/2511.08362},
}